Exercice 12 : Taille étudiants

Pour mettre en pratique ce qu'il a appris dans son cours de Statistique Inférentielle, un étudiant souhaite utiliser l'Approche Expérimentale pour comprendre la notion d'intervalle de confiance. Son but est d'estimer par intervalle de confiance la taille moyenne, notée $\mu$, des $N=300$ étudiants de sa promotion.
(1) Il construit un premier échantillon (avec remise) de taille $n=30$ (i.e. pour se placer dans le cadre asymptotique), qu'il note ${\bold{ y_{[1]} }}$, dans la population des $N=300$ étudiants de sa promotion :

R> y1
 [1] 165 179 171 178 171 168 166 171 182 178 177 165 174 164 175 178 167 168 185
[20] 166 162 180 167 174 159 159 184 154 172 157

Proposez l'instruction R ayant permis d'obtenir le résultat ci-dessous correspondant à un intervalle de confiance au niveau de confiance de $80\%$ de $\mu$ :

R> # IC <- (instruction R à fournir dans la rédaction)
R> IC
[1] 168.6308 172.4359

(2) Ne sachant pas comment interpréter ce résultat, il construit 19 autres échantillons de taille $n=30$ dans la population des étudiants de sa promotion que l'on notera respectivement ${\bold{ y_{[2]} }},\ldots,{\bold{ y_{[20]} }}$. Il représente alors sur un même graphique ces 20 différents intervalles de confiance de $\mu$ à $80\%$ de niveau de confiance :
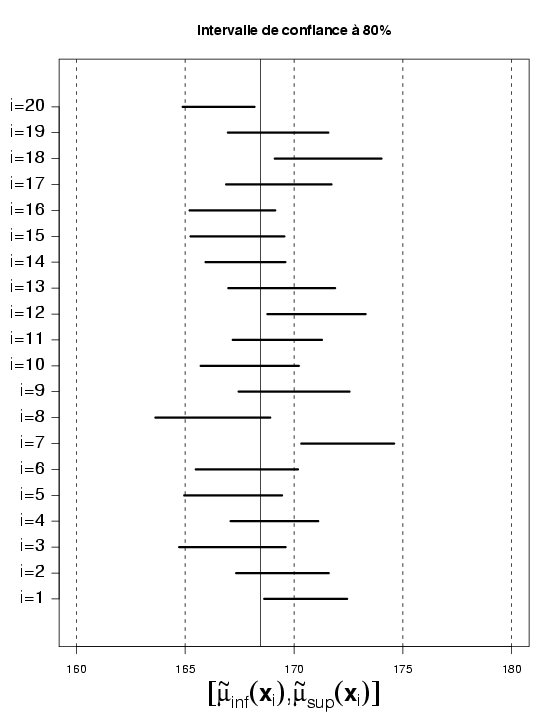
Afin de confronter ses résultats expérimentaux avec la réalité, l'étudiant décide d'interroger tous les étudiants de sa promotion (notez que ceci est possible car $N=300$). Il peut alors calculer la valeur de $\mu$, à savoir $168.45$. Elle est représentée par le trait vertical (en trait plein) sur le graphique précédent. Sur les 20 intervalles de confiance calculés, combien contiennent $\mu$ ? Est-ce surprenant ? Répondre à toutes ces questions en complétant le questionnaire suivant.
3) Que se passerait-il si l'étudiant construisait une infinité d'intervalles de confiance de $\mu$ à $80\%$ de niveau de confiance sur des échantillons de taille $n=30$?

Exercice 14 : Proportion d'acheteurs

Un industriel s'interroge sur la proportion d'acheteurs parmi sa clientèle qui ont acheté ou ont l'intention d'acheter le produit A, proportion notée $p^A$. En particulier, il souhaiterait construire un intervalle de confiance de cette proportion d'acheteurs $p^A$ obtenu à partir d'un échantillon de taille $n=500$ individus issus de la population de taille $N=2000000$.
(1) Proposez l'instruction R ayant permis d'obtenir le résultat ci-dessous correspondant à un intervalle de confiance au niveau de confiance de $90\%$ de $p^A$ calculé à partir du jeu de données ${\bold{ y }}$ que l'on note y en R (cet intervalle est noté $[\widetilde{{ p^A}}_{ inf}\left({\bold{ y }}\right) , \widetilde{{ p^A}}_{ sup}\left({\bold{ y }}\right) ]$:

R> # IC <- (instruction R à fournir dans la rédaction)
R> IC
[1] 0.1630267 0.2209733

(2) Le produit A est maintenant lancé sur le marché, et il a été alors possible d'évaluer le vrai paramètre $p^A$ à $18.9\%$. Pour essayer de faire comprendre à l'un de ses collègues comment il faut interpréter les intervalles de confiance (en particulier le précédent), le concurrent propose l'exercice pédagogique suivant. On construit une urne de taille $N=2000000$ boules dont une proportion $p^A=18.9\%$ sont numérotées 1 (les autres étant numérotées 0). On fait alors $199$ tirages de 500 boules au hasard au sein de cette urne. Les jeux de données créés sont donc de la même nature que ${\bold{ y }}$. Les $m=200$ jeux de données sont notés ${\bold{ y_{[1]} }}$, ${\bold{ y_{[2]} }}, \ldots, {\bold{ y_{[200]} }}$ (le premier ${\bold{ y_{[1]} }}$ correspondant à ${\bold{ y }}$). Pour chacun de ces jeux de données, on construit un intervalle de confiance au niveau de $90\%$ du paramètre $p^A$. Voici dans l'ordre des tirages quelques uns de ces intervalles :

pInf      pSup
  [1,] 0.1630267 0.2209733
  [2,] 0.1971384 0.2588616
  [3,] 0.2210000 0.2210000
...
[198,] 0.1649122 0.2230878
[199,] 0.1724662 0.2315338
[200,] 0.1573773 0.2146227

Parmi les $m=200$ intervalles de confiance, 179 contiennent le vrai paramètre $p^A$, qu'en pensez-vous ? Si l'on construisait une infinité d'intervalles de confiance, combien contiendraient le vrai paramètre $p^A$ ?
(3) Proposer sans justification les valeurs de probabilités suivantes

• $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[1]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[1]} }}\right) \right)$

   = 0%

   ≃ 80%

   ≃ 90%

   ≃ 95%

   = 100%

   = 100% ou 0%




• $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[2]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[2]} }}\right) \right) $

   = 0%

   ≃ 80%

   ≃ 90%

   ≃ 95%

   = 100%

   = 100% ou 0%




• $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ Y }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ Y }}\right) \right) $

   = 0%

   ≃ 80%

   ≃ 90%

   ≃ 95%

   = 100%

   = 100% ou 0%

(4) Pour un niveau de confiance de $95\%$ évaluer $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[1]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[1]} }}\right) \right)$

(5) Pour un niveau de confiance avait été de $80\%$ évaluer $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[2]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[2]} }}\right) \right)$

(6) Pour un niveau de confiance avait été de $95\%$ évaluer $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[2]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[2]} }}\right) \right) $

(7) Pour un niveau de confiance avait été de $80\%$ évaluer $\mathbb{P}\left( \widetilde{{ p^A}}_{ \inf}\left({\bold{ y_{[1]} }}\right) < p^A < \widetilde{{ p^A}}_{ \sup}\left({\bold{ y_{[1]} }}\right) \right) $

Exercice 15 : Election 2012

Avant le premier tour des élections, nous sommes souvent assaillis par de nombreux sondages. Le 13 mars 2012, deux instituts de sondages (IFOP et SOFRES) publient leurs estimations sur les intentions de votes pour deux candidats C1 et C2:

• Sondage IFOP ($n=1638$): $\widehat{ p^{C1} }\left({\bold{ { y^{I} } }}\right)=27\%$ et $\widehat{ p^{C2} }\left({\bold{ { y^{I} } }}\right)=28.5\%$
• Sondage SOFRES ($n=1000$): $\widehat{ p^{C1} }\left({\bold{ { y^{S} } }}\right)=30\%$ et $\widehat{ p^{C2} }\left({\bold{ { y^{S} } }}\right)=28\%$

(1) A la lumière de ce cours, nous proposons les mêmes résultats présentés à partir des intervalles de confiance à $95\%$ de niveau de confiance :

• Sondage IFOP: $IC_{{ p^{C1}}}\left({\bold{ y^{I} }}\right)=[24.85\%,29.15\%]$ et $IC_{{ p^{C2}}}\left({\bold{ y^{I} }}\right)=[26.31\%,30.69\%]$
• Sondage SOFRES: $IC_{{ p^{C1}}}\left({\bold{ y^{S} }}\right)=[27.16\%,32.84\%]$ et $IC_{{ p^{C1}}}\left({\bold{ y^{S} }}\right)=[25.22\%,30.78\%]$

Fournir au choix :

• la formule mathématique (générale) permettant d'obtenir l'intervalle de confiance d'une proportion $p$ s'exprimant en fonction de l'estimation $\widehat{ p }\left({\bold{ { y } }}\right)$ et de la taille d'échantillon $n$
  Réponse

  $$IC_{{ p^{\bullet}}}\left({\bold{ y }}\right)=\left[\widetilde{{ p^{\bullet}}}_{ \inf}\left({\bold{ y }}\right),\widetilde{{ p^{\bullet}}}_{ \sup}\left({\bold{ y }}\right)\right]=\widehat{ p^{\bullet} }\left({\bold{ { y } }}\right) \mp \delta^{+}_{lim,\frac\alpha2}\times \sqrt{\frac{\widehat{ p^{\bullet} }\left({\bold{ { y } }}\right)(1-\widehat{ p^{\bullet} }\left({\bold{ { y } }}\right))}n} $$
• la vérification à la calculatrice de l'obtention de l'un des intervalles de confiance ci-dessus (détails des calculs à fournir)
  Réponse

  Pour exemple IFOP candidat C1: $$IC_{{ p^{C1}}}\left({\bold{ y }}\right)=\left[27\% - 1.96 \times \sqrt{\frac{27\%\times 73\%}{1638}}, 27\% + 1.96 \times \sqrt{\frac{27\%\times 73\%}{1638}}\right] $$
• la formule R d'obtention d'un intervalle de confiance en fonction de pEst et n désignant respectivement l'intention de vote pour un candidat et la taille d'échantillon.
  Réponse

  $\mathtt{pEst+c(-1,1)*qnorm(0.975)*sqrt(pEst*(1-pEst)/n)}$

Application: exemple IFOP candidat C1 (dernière ligne évaluée comme réponse après validation bouton bleu)